什么是算法

算法：简单来说，算法就是通过一系列的计算步骤，用来将输入数据转换成输出结果。

算法的性质

有穷性‌：算法必须在有限步骤内结束，且每个步骤在合理时间内完成，避免无限循环。‌
‌确定性‌：每一步指令含义明确、无歧义，相同输入必得相同输出。‌
‌可行性‌：所有操作可通过基本运算（如加减、逻辑判断）在有限次内实现。‌
‌输入‌：算法有零个或多个输入，取自特定对象集合（如用户数据或初始值）。‌
‌输出‌：至少有一个输出，反映输入加工后的结果（如计算结果或状态）。‌

算法的正确性

正确性：一个算法是正确的，如果它对于每一个输入都最终停止，而且产生正确的输出。

正确性的证明方法

数学归纳法
循环不变式

循环不变式

三步法：初始化（循环前成立）→ 保持（一次迭代后仍成立）→ 终止（循环退出时结合不变式推出规格）。

例题

用循环不变式证明一下算法正确性：

循环不变式：

在第 $j$ 次迭代开始时（即尚未处理 $A[j]$ 之前），变量 $key$ 等于前缀 $A[1..j-1]$ 的最大值：

key=max\{A[1],A[2],...,A[j-1]\}

Step1：初始化

循环第一次迭代前 $j=2$ ，此时 $key \leftarrow A[1]$ ，显然：

key=A[1]=max\{A[1]\}

不变式成立。

Step2：保持

设在某次迭代开始时不变式成立，即：

key=max\{A[1],...,A[j-1]\}

现比较 $key$ 与 $A[j]$ :

若 $key < A[j]$ ，执行 $key \leftarrow A[j]$ ，此后 $key=max\{A[1],...,A[j]\}$
若 $key > A[j]$ ，不更新，仍有 $key=max\{A[1],...,A[j]\}$

因此本轮结束时， $key$ 成为前缀 $A[1..j]$ 的最大值，下一轮开始时索引变为 $j+1$ ，于是：

key=max\{A[1],..,A[j]\}=max\{A[1],...,A[(j+1)-1]\}

不变式对下一轮仍成立。

Step3：终止

当循环结束时， $j=n+1$ 。根据不变式，循环结束时刻 $key$ 等于：

max\{A[1],...,A[n]\}

也就是数组整体最大值。返回 $key$ 即满足规格（部分正确性）。

算法时间复杂度的估算

渐进复杂度

$\mathcal{O}$ 上界

如果 $f(n) \in \mathcal{O}(g(n))$ ，即 $f(n)$ 的数量级小于等于 $g(n)$

$\Omega$ 下界

如果 $f(n) \in \Omega(g(n))$ ，即 $f(n)$ 的数量级大于等于 $g(n)$

$\Theta$ 紧确界

如果 $f(n) \in \Theta(g(n))$ ，即 $f(n)$ 的数量级等于 $g(n)$

$o \space \omega$ 严格

例题1

定义：若存在常数 $C$ 、 $n_0$ 使得对所有 $n>n_0$ ， $f(n) \le C \cdot g(n)$ ，则 $f(n)=\mathcal{O}(g(n))$ 。

（1）证明 $f(n)=\mathcal{O}(n^2)$ ：

当 $n \ge 3$ 时，有 $3n \le n^2$ ，且 $1 \le n^2$ ，于是

f(n)=n^2+3n+1 \le n^2+n^2+n^2=3n^2

取 $C=3$ ， $n_0=3$ ，满足定义，故 $f(n)=\mathcal{O}(n^2)$ 。

（2）证明 $f(n)=\mathcal{O}(n^3)$ ：

当 $n \ge 1$ 时，有 $n^2 \le n^3$ ， $3n \le 3n^3$ ， $1 \le n^3$ ，于是

f(n)=n^2+3n+1 \le n^3+3n^3+n^3=5n^3

取 $C=5$ ， $n_0=1$ ，满足定义，故 $f(n)=\mathcal{O}(n^3)$ 。

例题2

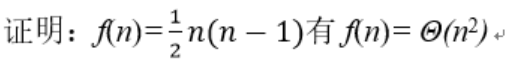
取 $n \ge 2$

下界：

\begin{aligned} f(n)&=\frac12 n(n-1)=\frac12 n^2-\frac12 n \\ &\ge=\frac12 n^2-\frac14 n^2 \\ &=\frac14 n^2 \end{aligned}

上界：

\begin{aligned} f(n)&=\frac12 n(n-1)=\frac12 n^2-\frac12 n \\ &\le=\frac12 n^2-0 \\ &=\frac12 n^2 \end{aligned}

于是存在常数 $c_1=\frac14$ ， $c_2=\frac12$ ， $n_0=2$ 使得

c_1n^2 \le f(n) \le c_2n^2 \space (\forall n \ge n_0)

故 $f(n)=\Theta(n^2)$

递归算法时间复杂度计算

递归方程

步骤：

定义T(n)：表示问题规模为n时的时间复杂度。
拆分递归过程：分析每次递归调用的子问题规模和操作次数。
建立递推方程：将T(n)表示为子问题的时间复杂度之和。
求解方程：通过代入法、递归树或Master定理得出结果。

递归树

步骤：

画出递归树：每个节点表示一个子问题，标注其规模和操作次数。
计算每层的时间复杂度：将每层所有节点的操作次数相加。
累加所有层的复杂度：得到总时间复杂度。

例题

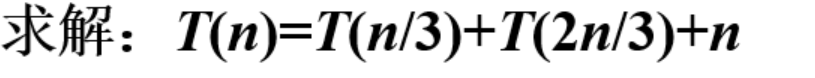
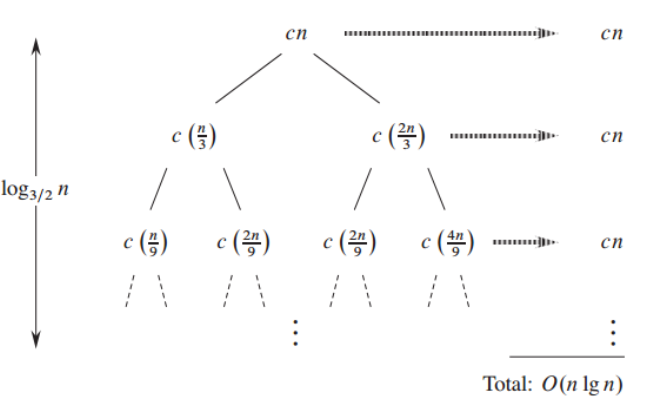
每一层把规模 $n$ 分成 $\frac n 3$ 和 $\frac {2n} 3$ 。从根到叶的最长路径总是走“更大的那支” $\frac {2n} 3$ ：

n(\frac{2}{3}) ^h \le 1 \rightarrow h \ge log_\frac{3}{2}n

设第 $k$ 层所有子问题规模之和为 $S_k$ 。根层 $S_0$ 。
把某个规模为 $s$ 的结点拆成 $\frac s 3$ 和 $\frac {2s} 3$ 后，新层的总规模贡献仍是 $s$ 。
对每个结点都如此，故

S_{k+1}=\sum s = S_k

归纳得每层 $S_k=n$ 。而本题每个结点的“合并/额外代价”与子问题规模成线性（记常数为 $c$ ），
所以第 $k$ 层总代价是 $S_k=c\,n$ 。

层数约为 $h=\Theta(\log_{3/2} n)$ ，于是内部结点总代价

\sum_{k=0}^{h} c\,n = c\,n\cdot \Theta(\log_{3/2} n)=\Theta(n\log n)

叶子层：每个叶子规模 $O(1)$ ，叶子个数不超过同层规模之和 $S_h=O(n)$ ，
总叶子代价 $O(n)$ ，被 $\Theta(n\log n)$ 主导。

结论： $T(n)=\Theta(n\log n)$

主定理

适用条件：递归方程形如 $T(n)=a \cdot T(\frac n b)+f(n)$ ，其中：

$a \ge 1$ ：子问题的数量
$b > 1$ ：每个子问题的规模缩小因子
$f(n)$ ：分解和合并子问题的时间复杂度

结论：

若 $f(n) < n^{log_b(a)}$ ，即 $\exist \varepsilon \gt 0$ ，有 $f(n)=\mathcal{O(n^{logb(a)-\varepsilon})}$ ，则 $T(n)=\Theta(n^{log_b(a)})$
若 $f(n) = n^{log_b(a)}$ ，则 $T(n)=\Theta(n^{log_b(a)} \cdot logn)$
若 $f(n) > n^{log_b(a)}$ ，即 $\exist \varepsilon \gt 0$ ，有 $f(n)=\Omega(n^{logb(a)+\varepsilon})$ ，且对 $\forall c \lt 1$ 与所有足够大的 $n$ ，有 $af(\frac n b) \le cf(n)$ ，则 $T(n)=\Theta(f(n))$

例题

（1）这里 $a=5$ ， $b=2$ ， $f(n)=n^2$

比较 $f(n)$ 与 $n^{log_b(a)}=n^{log_2(5)}\approx n^{2.322}$ 则 $\varepsilon \approx 0.322$

故 $T(n)=\Theta(n^{log_2(5)})$

（2）这里 $a=2$ ， $b=2$ ， $f(n)=n$

比较 $f(n)$ 与 $n^{log_b(a)}=n^{log_2(2)}=n$

故 $T(n)=\Theta(nlogn)$

Kyrie

绪论